End-Tagged Dense Code (ETDC) and SC-Dense Codes (SCDC) are the 2-pass (semistatic) compressors of the Dense Codes family [Brisaboa et al. Information Retrieval' 2007], and therefore they well-suited for the compression of natural language texts.
These compressors are known to be among the most interesting semistatic techniques due to its good compression ratio (around 30-35%), fast compression speed and mainly decompression speed (maybe the best choice), and also because of the possibility of searching the compressed text much faster than the original uncompressed text.
ETDC and SCDC were developed to improve the compression ratio of Tagged Huffman (TH) [Moura et al. ACM-TOIS 2000] while keeping all its search capabilities. In practice ETDC improves TH in around 2.5 percentual points and SCDC obtains still better compression. Actually, SCDC obtains compression ratios very close ( only +0.2 percentual points) to Plain Huffman (PH) [Moura et al. ACM-TOIS 2000], which is known to be optimal prefix-free semistatic compressor.
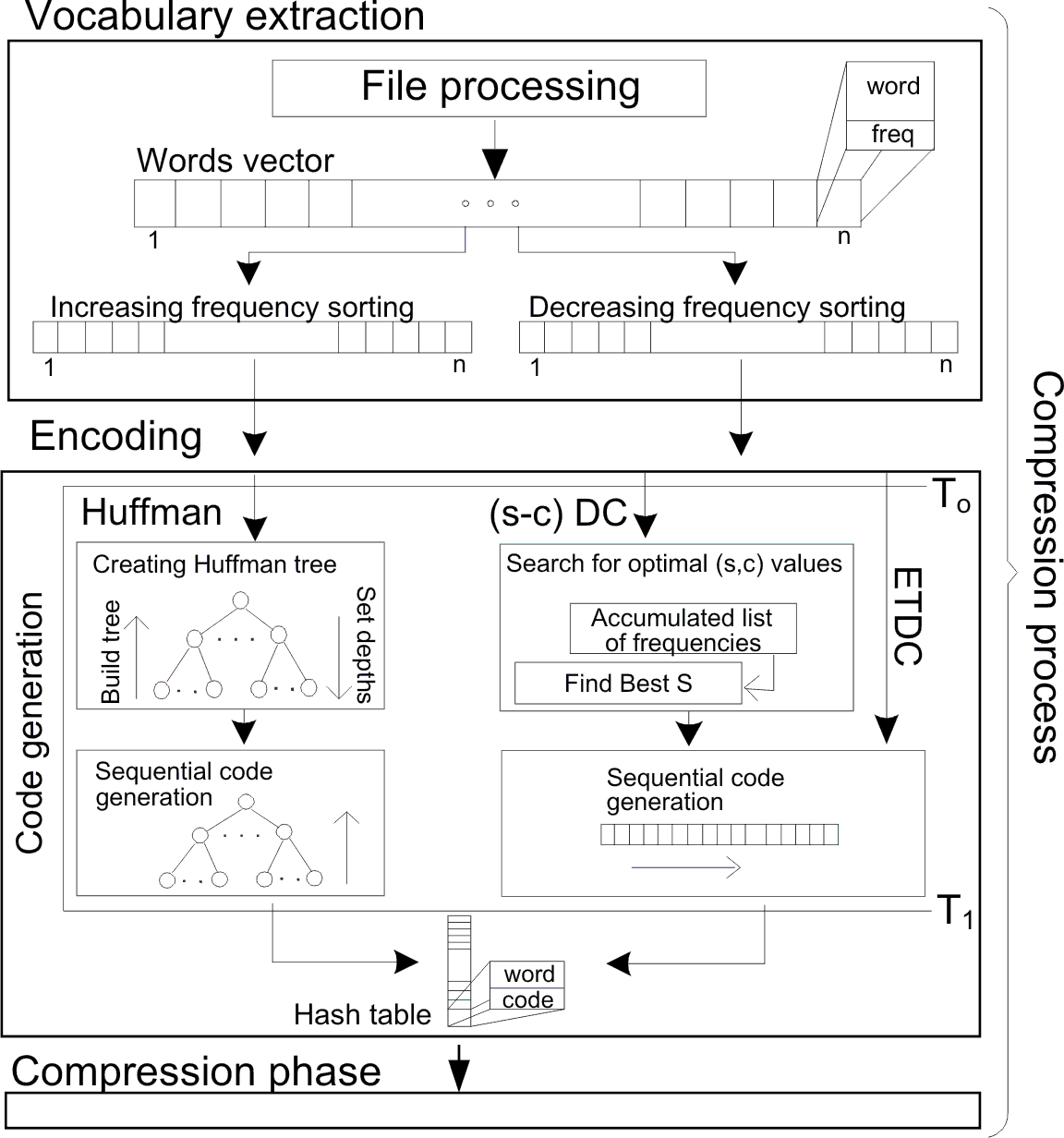
The structure of the these compressors is shown in the following picture.
If you want to know more about them, please refer to the publications section. In particular to the papers: [brisaboa et al. ECIR 2003], [brisaboa et al. SPIRE 2003], and the journal paper [brisaboa et al. Information Retrieval 2007].
If you are looking for the source code of such compressors then you might prefer to go directly to our download section.
ETDC and SCDC encode() and decode() procedures
Even though the Sequential code generation process is the the fastest way to generate codewords for all the words in a given vocabulary in the case of ETDC and SCDC, on-the-fly procedures are also available. Given a ranking in the sorted vocabulary "i", encode(i) outputs/returns the codeword associated to that position. Similarly, given a codeword "Ci", decode(Ci) returns the ranking in the vocabulary of the word associated to the codeword "Ci". These procedures are used in the case of our dynamic compressors: D-ETDC, D-SCDC, DLETDC and DLSCDC.
Next figures show the decoding and encoding functions for ETDC.


Next figures show the decoding and encoding functions for SCDC.


Where base[1]=0, base[2]=s, base[3]=s + sc, base[4]= s + sc+ sc2 ...